AN INTRODUCTION TO MUSIC THEORY
By Tom Irvine
Email: tomirvine@aol.com
November 24, 2000
________________________________________________________________________
Historical Background
Pythagoras of Samos was a Greek
philosopher and mathematician, who lived from approximately 560 to 480
BC. Pythagoras and his followers believed that all relations could be
reduced to numerical relations. This conclusion stemmed from
observations in music, mathematics, and astronomy.
Pythagoras studied the sound produced by
vibrating strings. He subjected two strings to equal tension. He then
divided one string exactly in half. When he plucked each string, he
discovered that the shorter string produced a pitch which was one
octave higher than the longer string. A one-octave separation occurs
when the higher frequency is twice the lower frequency.
German scientist Hermann Helmholtz
(1821-1894) made further contributions to music theory. Helmholtz wrote
"On the Sensations of Tone" to establish the scientific basis of
musical theory.
Natural Frequencies of Strings
A note played on a string has a
fundamental frequency, which is its lowest natural frequency. The note
also has overtones at consecutive integer multiples of its fundamental
frequency. Plucking a string thus excites a number of tones.
Ratios
The theories of Pythagoras and Helmholtz
depend on the frequency ratios shown in Table 1.
Table 1. Standard Frequency
Ratios
Ratio
|
Name
|
1:1
|
Unison
|
1:2
|
Octave
|
1:3
|
Twelfth
|
2:3
|
Fifth
|
3:4
|
Fourth
|
4:5
|
Major Third
|
3:5
|
Major Sixth
|
|
These ratios apply both to a fundamental
frequency and its overtones, as well as to relationship between
separate keys.
Consonance
Now consider two strings which are plucked
simultaneously. The degree of harmony depends on how the respective
fundamental frequencies and overtones blend together.
Music notes which blend together in a
pleasing manner are called consonances. Notes with a displeasing blend
are dissonances.
Helmholtz gave a more mathematical
definition of these terms:
When two musical tones are sounded at the
same time, their united sound is generally disturbed by the beats of
the upper partials, so that a greater or less part of the whole mass of
sound is broken up into pulses of tone, and the joint effect is rough.
This relation is called Dissonance. But there are certain determinant
ratios between pitch numbers, for which this rule suffers an exception,
and either no beats at all are formed, or at least only such as have so
little intensity that they produce no unpleasant disturbances of the
united sound. These exceptional cases are called Consonances.
Helmholtz has defined degrees of
consonance as shown in Table 2.
Table 2. Consonances
Degree
|
Interval
|
Absolute
|
Octave, Twelfth, Double
Octave
|
Perfect
|
Fifth, Fourth
|
Medial
|
major Sixth, major Third
|
Imperfect
|
minor Sixth, minor Third
|
|
For reference, a glossary of musical terms
is given in Appendix A.
Octave
Again, a one-octave separation occurs when
the higher frequency is twice the lower frequency. The octave ratio is
thus 2:1
A note's first overtone is one octave
higher than its fundamental frequency.
Consider a modern piano keyboard. The
beginning key on the left end is an A0 note with a fundamental
frequency of 27.5 Hz. A piano key has harmonic overtones at integer
multiples of its fundamental frequency. Thus, the A0 key also produces
a tone at 55.0 Hz, which is one octave higher than the fundamental
frequency. The second overtone is at 82.5 Hz.
The twelfth key to the right of A0 is A1,
counting both the black and white keys. The A1 note has a fundamental
frequency of 55.0 Hz. The A1 note is thus one octave higher than the A0
note, in terms of their respective fundamental frequencies. In fact,
there is a one-octave separation between any two piano keys which are
twelve keys apart.
A pleasing, harmonious sound is produced
when two notes separated by one octave are played simultaneously on a
piano or other musical instrument. Helmholtz calls such a pair an
absolute consonance. Thus, the A0 and A1 keys are an absolute
consonance.
This effect is shown for the A0 note and
the A1 note in Table 3.
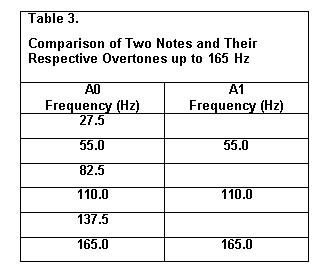
The overtones of the A1 note thus coincide
with the evenly numbered overtones of the A0 note. Again, these two
notes are separated by one octave.
Hermann Helmholz wrote:
A note accompanied by its Octave
consequently becomes brighter in quality, because the higher upper
partial tones on which brightness of quality depends, are partially
reinforced by the additional Octave.
Twelfth
A twelfth is two notes which form a
frequency ratio of 1:3.
A note's second overtone is a twelfth
higher than its fundamental frequency.
Recall the A0 note with its fundamental
frequency of 27.5 Hz. Its second overtone is 82.5 Hz, which is three
times higher than its fundamental frequency.
Ideally, there would be a key with a
fundamental frequency of 82.5 Hz. The nearest is the E2 key which has a
fundamental frequency of 82.407 Hz. This frequency approximately meets
the goal. Thus, the E2 key is considered as a twelfth higher than A0. A
comparison is shown in Table 4.
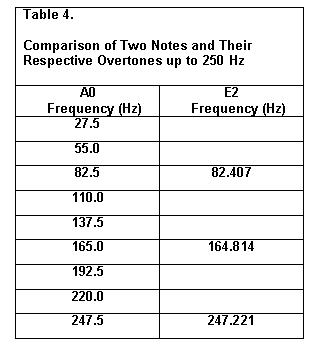
Thus A0 and E2 have three tones very
nearly in common in the frequency domain up to 250 Hz.
Fifth
A fifth is two notes which form a
frequency ratio of 2:3.
A note's second overtone is a fifth higher
than its first overtone .
Recall the A0 note with its fundamental
frequency of 27.5 Hz. A fifth higher would be 41.25 Hz. Such a note
does not exist in an exact sense. On the other hand, the E1 note has a
frequency of 41.203 Hz, which is approximately equal to the exact
fifth. Thus, E1 is considered as a fifth higher than A0. A comparison
is shown in Table 5.
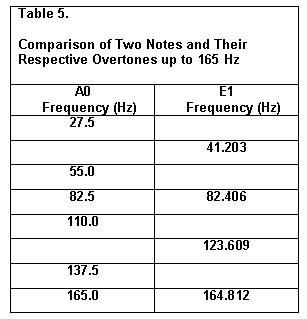
Thus, A0 and E1 have two overtones very
nearly in common in the frequency domain up to 165 Hz.
Reference
APPENDIX A
Glossary
Consonance - a simultaneous combination of
sounds conventionally regarded as pleasing.
Dissonance - a simultaneous combination of
sounds conventionally regarded as lacking harmony.
Harmony - a combination of musical
considered to be pleasing.
Harmonic - a tone in the harmonic series
of overtones produced by a fundamental tone.
Harmonic Series - a series of tones
consisting of a fundamental tone and the overtones produced by it,
whose frequencies are at integral multiples of the fundamental
frequency.
Interval - the difference in pitch between
two musical tones
Octave - the interval of eight diatonic
degrees between two tones, one of which has twice the frequency as the
other.
Overtone - a harmonic.
Partial - a harmonic.
Pitch - the frequency of a tone.
Reference: American Heritage Dictionary,
Houghton Mifflin Company, Boston, 1982.
|


